Sri Shyama Shastry – Music-continued
Varnas

Varna is a short, crisp and tightly knit composition that aims to encapsulate the main features and requirements of a Raga. These are finely crafted exquisite works of art. The creation of a Varna calls for delicate craftsmanship, thorough knowledge of the Raga, its sanchara (movements) in various Kaala (tempos) ; and, a grasp over Taala and an overall sense of beauty and balance.
Varna is unique to Karnataka Samgita. The Hindustani Music does not seem to have its counterpart
*
During the course of training in Music, after the Gitas, the Svarajatis with their rather complicated arrangement of Svaras and Sahitya are taught. Then comes the Varna; rich in textual expressions of Raga-Svarupa, displaying the vigour, the tenderness and the graces of the Raga.
Now, the student is at a more difficult level. She/he will have to gain an understanding of the subtleties involved in the rendering of a Raga in all its gaits and rhythms (Laya) through its ascending and descending notes, in Vilamba-kala (slow speed), in Madhyamā-kala (normal) and in Druta-kala (fast tempo) movements.
While doing so, the student learns to appreciate the unique characteristics of the dominant notes; and, the way they are used to delineate the Raga in its various shades and colours.
For students, the Varnas that are taught at the intermediary level are useful for learning the Svaras of various Ragas, singing in multiple speeds fluently; as well as learning the appropriate Gamakas.
Further, learning to sing effortlessly in three degrees of speed strengthens ones Laya-Jnana (sense of rhythm); while the profusion of vowels helps one to render Gamakas in smooth, seamless curves , oscillations, glides and turns.
Varna- rendering also helps to develop voice culture and in learning to maintain proper pitch and control over rhythm. The instrumentalists too can gain control over playing -techniques
Therefore, among the Music-curriculum, practicing Varna, understating its structure and its implications is of much importance. A diligent student, of both the vocal and the instrumental music, learns with great care and assiduity the various components (Anga) of the Raga structure and its nature.
*
[Smt Vedavalli, commenting on the pivotal role of Varnams, says, ‘When we come to Varnam that is when the kalapramanam will ‘kick’(trip us up). Varnams are actually more complex than Kritis (songs) to sing with fidelity to kalapramanam. When the student completes the Pallavi and Anu Pallavi in the first speed and starts the second speed after Muktayi svaram, the ‘running’ will happen. Difficult to determine why it happens, but it happens. The analogy is similar to the fact that it is difficult to see the minuscule increase in height of a growing plant or child on a daily basis, but it becomes noticeable when there is enough of a change. And for some reason, even if the first speed is started at a slow pace, the second speed instead of being its double, tends to become faster. Senior teachers used to say that the tendency for a beginning student to run in music is similar to the tendency of a small child to run very fast since they have not yet mastered the ability to calibrate their speed; something similar happens when learning to sing. The teacher has to keep calling this out to increase the awareness of the student when there is even a minute deviation in the tempo that needs to be maintained.
Even today in concerts, after the Tani Avartanam (percussion solo), and the musicians come back to the kriti, it is a natural occurrence for the tempo to have increased a little bit. But, if there is too much increase in second speed and then third speed is decreased to adjust, then it goes askew. Hence, it is extremely important when learning to be mindful of kalapramanam and to internalize it. To keep practicing with awareness and carefully checking that the same tempo is being maintained. Then, we can experience this ourselves.]
**
Although the Varna precedes the Kriti, in the teaching-schedule, the student continues to practice Varnas along with the Kritis, because of its inherent merit as an Abhyasa-gana
Therefore, in order to gain a convincing hold over a Raga and the Laya, a Varna in which its Raga-svarupa is crystallized in a systematic manner, the advanced students also practice Varnas in multiple Ragas or Taalas. It also helps to inculcate in them the discipline that is needed for singing complicated combinations of Svaras and Sahitya.
A Varna, therefore, is a very important component of both the Abhyasa-gana (compositions forming a part of initial training) and the Sadhana-gana (performance of the compositions);
In the concerts, a Varna is most often the first or the second piece to be rendered. Though some consider it as a warm-up exercise, the correct rendering of Varna requires complete knowledge of the Raga. It is thus of great value to beginner as also to and an experienced performer.
*
In the Karnataka Samgita, all types of compositions are Raga-specific. Among the many such verities, in particular, the Varna and the Kriti aim to bring out and display artistically, the nature and the tendencies of a Raga.
But, in a Kriti which is steeped in its own emotional content and in the intricacies of Prosody (Chhandas), Prasa, and Anuprasa etc., only certain aspects and shades of a Raga are portrayed, keeping in view the overall context of the Kriti.
The Varna, in contrast, is an independent and a methodically structured work having the sole aim to present efficiently and objectively all the significant characteristics of a Raga. Encapsulating and preserving the essentials, within a tight knit work of art, is the sole objective of a Varna. Apart from that, it has no other theme.
*
A Varna is composite musical form. According to one definition; it is said to include in itself the elements of Raga-Bhava; Raga-viseha-sancharas; and, several Apurupa- prayogas (use of unusual phrases in a Raga). Analysing and understanding these aspects are the initial steps in Manodharma Samgita.
Varna lays out the Grammar of a Raga. That is to say, it specifies the features and the rules regarding the movement of the Raga (Raga-sanchara); its scale; how each note of the Raga should be stressed and so on. A Varna is therefore a fundamental form in Karnataka Samgita.
Learning a Varna is the process of getting to know intimately a Raga, which is beautified by the tonal excellence of its Svaras. Each Raga has its own peculiar features; it is a living and a throbbing dynamic entity finding its own flow, rhythm and gait. Each one has its own preferred ways of movements, turns, slides and glides etc.
*
In a Varna, the starting note of its Pallavi is said to be significant; because, it captures the flavour of the Raga, and establishes its identity. It is also said; the identity of a Raga is better established in the Avaroha (descent), especially in the Madhya-Sthayi.
A Varna attempts to project the total picture of a Raga, drawing attention to its parentage (Mela), its Murchanas (the ascending and descending movement of the seven notes in successive order) , pointing out to its Graha-Svara (initiating Svara), its Amsa Svara – the important notes ,which should be prolonged; the Hrasva-Nyasa, the shortened delicate notes at the conclusion of a phase; and so on.
The Varna also tries to demonstrate the enterprising Ranjaka-Prayogas, Viseha-Sancharas, permissible Apurva-Prayogas; Dhathu-Varisha-Prayogas and the Alpa-Prayogas– the skipping of certain notes etc.
In short, a Varna captures the total physiology of a Raga within a well designed work of Art.
*
A Varna does include Sahitya (lyrics); but, its role is rather secondary; mostly supporting the music-content of the Varna. It provides the Lakshya and Laksana of a Raga. The focus of a Varna is on the Raga, its individual Svaras and Svara phases of various lengths and speeds. It is said; a Varna does not need the distraction of Sahitya.
*
Usually, there will be two Avartas (cycles) each for Pallavi and Anupallavi; and, two to four Avartas for the Muktayi-Svaras. The length of the Ettugada Svaras increases progressively; and, the last Svara will be the longest one. This will have four or five Ettugada Svaras.
The movement of a Varna is strictly controlled; and, it’s rendering demands discipline. Its focus is on the Graha Svara (initial note of the Raga), the Gamakas, the Sanchara (movement) of the Raga according to the prescribed format.
The Pallavi of a Varna starts on the lower end of the scale, stressing on the most important Svara (Jiva Svara) in the opening phase of the Pallavi. The Anupallavi deals with the higher end of the scale. And, the Mukthayi Svara and Chittasvara – consist of meandering (Sanchari) chains of Svaras that explore both the upper and lower reaches of the Raga.
The rendering of a Varna employs all the three tempos. The first Carana-Svara is rendered in Vilamba-kaala (slow tempo); where, each Jiva Svara must be highlighted.
After which, the rest is sung in Madhyamā-kaala (half-time). Some musicians insert their own kalpana-svara passages.
In the third Carana-Svara, the Svaras are short and made into groups (Avartana) of four.
Thus in Carana, there are two or three Svaras of one Avartana, one Svara of two Avartanas; and, finally one Svara of four Avartanas.
*
The Varnas are mainly of three types: Daru-Varna, Pada-Varna and Taana-Varna. The theme of these Varnas is usually Bhakthi (devotion) or Srngara (love).
The major types of Varnas are, however, two: Taana-Varna and Pada-Varna.
The Taana-Varna, with Svara and Sahitya passages, is essentially for concert Music. The Pada-Varna, with its rhythmic patterns, is mainly for Dance.
[There is also a mention of Raga-maalika-Varnas, with a string of stanzas, composed in compatible Ragas that blend well with each other. This type could be either Taana-Varna or Pada-Varna.
The other is the Nakshatra-malika-Varna, set in twenty-seven Ragas (each representing a star in the Indian Almanac) . In each Avartana, the first half is set in one Raga; and, the second half in another Raga; which makes two Ragas in, one Avartana.]
*
Daru-Varnas are a special type of Varnas, wherein its Mukthayi-Svaras start with the Svara passages, followed by the Jatis, which are then followed by the Sahitya. The Daru Varnas are structured with Ettugada-Pallavi and Ettugada-Svara-passages. They are similar to the Pada-Varnas; and, are well suited for Dance.
[ Maathe Malayadhwaja Pandya-sanjathe (Raga Khamas) by Sri Mutthaiah Bhagavatar , a Vidwan of the Royal Court of Mysore, is a celebrated example of a Daru Varnam. Please click here for it rendering by the students of Samt.Ranjani and Smt.Gayatri ]
*
Pada-Varna (Ata-Varnam): As its name indicates, has a greater element of Sahitya (Pada or words). Pada-Varnas with elaborate Sahitya are hard to grasp; especially, when set to difficult Ragas and Taala.
But, the Pada-Varnas rendered in Vilambita-laya, offer greater scope for Abhinaya to interpret the Sahitya, interspersed with appropriate Sollulkottus, Tirmanas and stances. Hence, they are in greater use in Bharatanatya; where, it’s Sahitya, its expressions and its Svaras, in moderately slow pace, are said to be suitable for choreography.
[Pada Varnas used for dance choreography are also called as Chowka Varnas or Ata Varnas. They usually are set in slower tempo (Chowka-kala); and, have longer lines and pauses, enabling the apt portrayal of the Bhava of the Varnam. All its Svaras are accompanied by Sahitya (lyrics) and Sollukattus which are made up of rhythmic syllables. The dancer performs the Sahitya in Abhinaya and the Sollukattus in Nrtta. Thus, the Chowka Varnas are well suited to dance.
Further, learning to sing Chowka Varnas is considered a part of developing a good voice culture. The Chowka kala rendering helps one to explore the Raga, in depth. It also helps the learner to balance the Taala; to adjust the Gamakas; and, to pay greater attention to pauses.]
*
[When adopted into Dance-form, Varnam is transformed into the richest composition in Bharatanatya. The Varnam, either in music or dance, is a finely crafted exquisite works of art; and, it gives full scope to the musician and also to the dancer to display ones knowledge, skill and expertise.
And , in Dance , its alternating passages of Sahitya (lyrics) and Svaras (notes of the melody) gives scope to the dancer to perform both the Nrtya (dance with Abhinaya) and Nrtta (pure dance movements) aspects. In its performance, a Varnam employs all the three tempos. The movement of a Varnam, which is crisp and tightly knit, is strictly controlled; and, it’s rendering demands discipline and skill. It also calls for complete understanding between the singer and the dancer; and also for the dancer’s ability to interpret not only the words (Sahitya) but also the musical notes (Svaras) as per the requisite time units (Taala). The dancer presents, in varied ways, through Angika-abhinaya the dance elements, which the singer brings forth through the rendering of the Svaras. ]

The Taana-Varna perhaps derived its name on account of its brisk Laya and Svara arrangements with pulsating movements in even tempo, as in the Taanam. It usually is of fast tempo (Druta and Tisra Gati). But, they sound best in Madhyama-kala, when the Taana sequences have to be executed.
Taana-Varnas do not have Sahitya for Svaras. It is the sort of Varna that is meant as pure music, without the intervention of words. It, therefore, has fewer words than the Pada-Varna.
The characteristic Svara-Prayogas, emphasising on Graha, Nyasa, Amsha; as well as Hrsva, Deergha–Prayogas are very frequently employed in Taana-Varna.
The difficult Taana-Varnas are commonly chosen for rending in the concerts; and, they provide the base for Mano-dharma-samgita. The artists enjoy greater elaborations of Taana-Varnas studded with Kalpana-Svaras to enhance to beauty of the Raga; and, to entertain the listeners.
*
A typical structure of a Taana-Varna has Pallavi, Anupallavi, Mukthayi Svara, Carana, Carana-Svara and an optional Anubandha.
A Varna is structured in two Angas (sections):
The Purvanga (first section) comprises Pallavi, Anu-pallavi, Mukthayi-Svara (a passage of Svara syllables, usually of two Avartas, succeeding the Anupallavi).
And, the Uttaranga (the latter section) comprises a Carana that acts as a refrain for the latter part of the Varna and Carana-Svaras (Chittasvara) that are alternated with the Carana.
Each section of a Varna elaborates an aspect of the Raga (raga-svarupa).
Thus, the Taana-Varnas are basically Svara and Sahitya exercises; and, help the student to gain a greater degree of control while venturing into the finer Prayogas in the Raga.
*
Gana-krama
Although the Varna has the structural divisions of Pallavi, Anupallavi (with Muktayi Svara) and Carana; while singing, the Pallavi is not treated as an independent Anga. There is continuity in singing.
The Purvanga starts with the Pallavi; and, is continued through Anupallavi and Mukthayi Svara; and, then it reverts to the opening words of the Pallavi.
The first movement of the Pallavi ends in Mukthayi-Svara. After this, the Ettugada Pallavi, made of the Sahitya lines of the Carana, is sung. This is followed by the Svara-passages in sequence. After each Svara passage, the Carana line is sung again, as refrain
[It is said; in the olden days, the Purvanga was sung in all the three speeds followed by Uttaranga, alternating between two speeds for each Carana. Nowadays many other rendition styles have come into being.]
[Sometimes a Taana-Varna is adapted for dance (Say, like Viriboni, Bhairavi, Ata). In such cases, the Taana Varna is expanded by repeating the Sahitya many times, with Sangatis. Additional Sahitya and Jati patterns are added. And, even though the words are meagre, the dancer has to interpret them with Abhinaya, so that the meaning is brought out clearly. ]

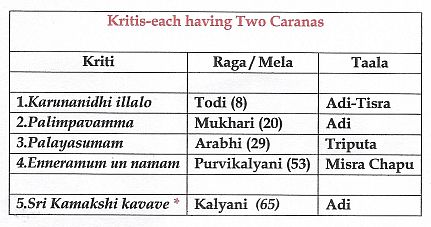
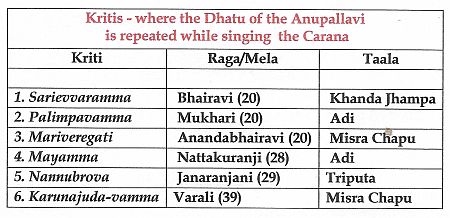
The Varnas composed by Sri Shyama Shastry
According to most of the versions that are now in circulation, Sri Shyama Shastry is credited with four Varnas, which are highly musical in their structure. They are:
(1) Na-manavi-vinu (Saurastra-Chatursra-Ata); (2) Samini-ramm-anave (Anandabhairavi, Khanda-Ata); (3) Dayanidhe (Begada, Adi); and, (4) Nive-gatiyeni (Kalyani, Tisra-Mathya).

[Though most of the sources mention these four Varnas as the works of Sri Shyama Shastry, Smt. Sharadambal recognized only two Varnas (not four) as that of Sri Shyama Shastry.
She says: ’There are two Varnas of Sri Shyama Shastry found in the early publications’. And, throughout her book, she talks of only about his two Varnas; Samini-rammanave (Anandabhairavi, Khanda-Ata) and Dayanidhe (Begada, Adi).
She also mentions that the detailed notations have been worked out for the Varna ‘Samini…’ (Anandabhairavi) in the Sangita-Sampradaya-Pradarshini of Sri Subbarama Dikshitar at B.50 on pages 1540-1545.
This and the Hand Written Note Book of Shyama Shastry II are said to be her sources.
According to Smt. Sharadambal, both these Varnas are Taana Varnas. Yet, in the Varna ‘Samini-rammanave’ (Anandabhairavi), the Sahitya resembles Pada-Varna. This is sung by the Nayaki to her Sakhi, to describe her plight to Lord Varadaraja of Kanchipuram, who is the Nayaka of the Varna.]
*
These four Varnas, though similar to Svarajati (pertaining to the realm of Dance), in structure; they are composed of a separate Pallavi, Anupallavi and Mukthayi- Svara, collectively known as Purvanga. The Uttaranga part consists of Carana, Carana-Svaras and Sahitya.
These Varnas are above the level of the usual Abhyasa-gana–Varnas. They are set in more difficult Taalas, like Chaturasra Ata and Tisra Mathya. The Varnas here, are characterized by many peculiar features, such as: the introduction of Svara-Sahitya (each Svara syllable having a corresponding syllable of text of identical duration) in the Mukthayi-Svara (in ‘Na-manavi’ and ‘Dayanidhe’); and, the unusual length of the Carana-Sahitya (four Avartas in ‘Nive-gatiyani ‘, Kalyani)’
The Varnas in Kalyani and Anandabhairavi are recommended even for the practitioners at a slightly higher level.

- The Varna Na manavini vinu in Raga Saurastra is set in Chatursra Ata Taala.
[Raga Saurashtra is a Janya of the 17th on the Melakarta Suryakanta
Arohana (Ascending): S R1 G3 M1 P M1 D2 N3 S’ / Avarohana (Descending) : S’ N3 D2 N2 D2 P M1 G3 R1 S.
Saurastra is an auspicious Raga. Sri Thyagaraja’s opera ‘Prahlada Bhakthi Vijayam’ opens with ‘Sri Ganapathi’ and concludes with the Mangalam’ Nee Nama Rupamalu’ both of which were set in Raga Saurastra.]
The Varna is structured with a Pallavi, Anupallavi followed by a Svara-Sahitya passage; and ends with a short Carana of just two lines.
Na Manavi Vinu yi vela brovu Kanchi Kamakshamma / Pamara-palini O Janani, krupa judamma is a poignant prayer submitted to Kanchi Kamakshi , beseeching her, repeatedly, to kindly show mercy and to pardon him for all his wrong-doings committed knowingly or otherwise (telisi-telitaka-jesina-aparadhamulanu-manninchi); to protect him (brovu) ; and ,to grant him salvation (Mukthi ni eeyave). O Mother, I have the deepest faith in you; I trust you, I trust you and have ever trusted you (nammiti nammiti nammitin-amma).
The slower tempo (Chowka-kala) and Chatursra-Taala are eminently suited for the Raga-Bhava of Karuna Rasa. Usually, such Varnas in Chowka-kala will have longer lines and pauses, enabling the apt portrayal of the Bhava of the Varnam.
This Varna has two Avartas (Taala-cycles) each, in the Pallavi and the Anupallavi. The Svara-Sahitya passage is appended to the Muktayi Svara. The introduction of the Tisra, Chatursra and Khanda groups in patterns can be seen in this Varna.

- The Varna Samini-ramm-anave Saraskshi is set in Raga Anandabhairavi, Ata Taala
[Anandabhairavi is a Janya of the 22nd Mela Kharaharapriya. Arohana: S G₂ R₂ G₂ M₁ P D₂ P Ṡ / Avarohaṇa: Ṡ N₂ D₂ P M₁ G₂ R₂ S.
Svara-sthanas: Chathusruthi-Rshabha, Sadharana-Gandhara, Shuddha-Madhyamā, Chatusruthi-Daivatha, Kaisiki-Nishada; apart from Shadja and Panchama.
Anandabhairavi is said to be one of the favourite Ragas of Sri Shyama Shastry.]
Saminirammanave (Anandabhairavi) is an Ata-Taala, Taana-Varna, starting in the Laghu after a pause of eight Akshara-kala duration.
But, here, the Svarasahitya passages are suffixed to the Muktayi-Svara, first, fourth and fifth Ettugada-Svaras. There are five Ettugada Svaras in all. Few syllables are there in the Pallavi and Anupallavi, with more vowel extensions.
This Varna is marked by a number of distinct features.
This is a fairly lengthy Varna with Pallavi, Anupallavi and two Caranas, with four Svarasahithya passages interposed between the Anupallavi and the last Carana.
Though it is listed under Taana-Varnas, its Sahitya resembles Pada-Varna.
We find the Kshetra-mudra ‘Kanchi-vasudina-Sri Varadarajuni’ in the Anupallavi.
The Telugu language used in this Varna is different from the one found in his Kritis. The use of the complex words of archaic poetic nature resemble the Svarajatis; and gives a complex form to the language, as against the simple colloquial style of the Kritis. In fact, the Telugu Sahitya here makes a difficult reading.
*
And, to say the least, this is a rather unusual Varna; and, therefore, has been much discussed.
This is one of the two compositions of Sri Shyama Shastry that is not dedicated to praise the Mother Goddess in her various forms.
This Varna is the only single instance among the body of the works of Sri Shyama Shastry portraying Madhura-bhakthi.*
*
Sri Shyama Shastry was a true Bhaktha of the Devi in the classical mould. He worshiped his Ishta-Devatha Bangaru Kamakshi with intense devotion (Archana); serving her and praying at her feet (Pada-sevana, Vandana and Dasya); thinking of her all the time (Smarana); listening to the legends of her magnificence (Srvavana); singing of her beauty, glory and splendour in countless manners (Kirtana); submitting himself to the will of the Mother and seeking refuge in her with absolute faith (Atma-nivedana) .
Thus, Sri Shyama Shastry was indeed a true icon of a devotee, a Sadhaka who constantly served his Devata with utmost devotion in all its modes (Nava-vidha-Bhakthi) as extolled in the Srimad Bhagavatha Purana.

Shravanam, Kirtanam , Smaranam, Paada-sevanam, Archanam, Vandanam, Daasyam , Sakhyam Aatma-nivedanam
*
Sri Shyama Shastry adopted the Apatya-bhava*, an intense sense of proximity, looking upon Devi Kamakshi as his own Mother, who is always with him. It is the guileless (Akritrima) natural love; the purest of the attitudes that one can cultivate towards God.
[* The term Apatya is related to the child; and, to its attitude towards its parents. Yaska, in his Nirukta 3.1 :, explains it as: apatyaṃ kasmāt apatataṃ bhavati pituḥ sakāśādetya pṛthagiva tataṃ bhavati. ]
He was a child (Bidda, Sutudu) to his mother (Talli, Mayamma) with whom he talked, confided his fears, argued with her, cajoled her, persistently sought her protection ; and , above all, he never was willing to be weaned away from her. He loved her with all his heart, as only an innocent child can. He devoted his entire adult life in serving her, thinking of her, being ever dedicated to her, and loving her till his very last moment on this earth.
[Sri Shyama Shastry could foresee the end of his time on this Earth.
On the morning of the that appointed auspicious day, the Dashami, Tuesday (Cevvai), Shukla-paksha Makara (Magha) Masa , Shishira-Rtu – Uttarayana – Vyaya – Samvatsara – 1748 – Kaliyuga – 4927, February 7th, 1827, Sri Shyama Shastry meditated upon his Ishta Devata Mother Kamakshi; and, a little later he laid his head on the laps of his son Subbaraya Shastri; and, asked him to softly recite the Karna-mantra into his ears.
He was fully conscious till the very last moment. He peacefully, serenely journeyed to Sripuram; the heavenly abode of Devi Kamakshi, as if a child goes home to his Dear Mother.
That was how a noble soul came to pass.]

The other notable Sadhaka who adopted such Apatya-bhava was Sri Ramakrishna Paramahamsa (18 Feb 1836 – 16 Aug 1886), who was born about nine years after the passing away of Sri Shyama Shastry (1827).
Sri Ramakrishna, just as Sri Shyama Shastry, was a priest. He worshipped Goddess kali at the Dakshineshvar temple. And, he too regarded Kali as a living Goddess (Pratyaksha Devata); he felt her presence everywhere, talked to her, fed her, and argued with her just as a child does with its loving Mother.
[The other Sadhakas who sang of Kali with a flaming devotional fervour that quickly come to my mind are Ramprasad Sen (1718-75) and Kamalakanta Bhattacharya (c. 1769–1821)]
*
Sri Ramakrishna all through his Sadhana-kala practiced Apatya-bhava. But, for a very brief time, he tried, Madhura-bhakthi-bhava, the sweet love-filled attitude (Mahabhava) of Radha, the highly idealized personification Love and Beauty, towards Krishna the eternal Lover.
But, very soon he came back to Santa-Apatya-Bhava, the child-attitude, of peaceful adoration.
*
In all the known compositions of Sri Shyama Shastry that have come down to us, it is the Apatya-bhava, the love and affection binding the child and the Mother that shines forth and overwhelmingly dominates. His child-like love, looking up to Devi Kamakshi as his own Mother; as also the Bhakthi and Karuna Rasa appealing to her for love and care at every moment and every turn of his life are the recurrent themes of all his compositions. It is truly very touching. And, when that purest emotion is rendered through soulful Vilamba kala, it is then the Bhakthi Samgita of the highest order.
The Varna in Anandabhairavi is the sole instance of Madhura Bhakthi among all his compositions.
This could be considered as a very brief phase along the course of his Sadhana, which was essentially rooted in the Apatya-bhava, the purest of all. Just as Sri Ramakrishna did later, Sri Shyama Shastry had quickly come back to his own natural aptitude. You can perhaps say; Apatya, truly, was Sri Shyama Shastry’s Sthayi-Bhava; while Madhurya was a fleeing Sanchari-Bhava.
*
The Varna Samini-ramm-anave (Anandabhairavi), for all purposes can be treated as a Pada Varna.
This is sung by the lovelorn (Virahini) Nayaki, asking her maid (Sakhi), to convey a message (Sandesha) to her Lord Varadaraja of Kanchipuram, the Nayaka, describing her plight, suffering pangs of separation; and, hasten to come to her.
Here, in this Varna, there are descriptions of the Lord as ‘Kamini Kanna’, who gave birth to Manmatha; and as Gunavanthudaina (meritorious one) Sarasa-nayana (with eyes like lotus), Samaja-gamana (with gait like that of an elephant).
*
Some have pointed out that considering the overall nature of Bhakthi and Karuna Rasa, that pervades the compositions of Sri Shyama Shastry, the Varna ‘Samini..,’ surely does appear to be out of character; and, it stands out oddly. Therefore, they have expressed reservations about the authorship of this Varna; and, have even pondered over the possibility that it might have been, at a later stage, interpolated (prakshepa) by someone else into the body of the works of Sri Shyama Shastry.
That is a fairly plausible way of looking at this Varna, in the context of Sri Shyama Shastry’s compositions taken as a whole.
But, the scholars such as Prof. Sambamoorthy (1930), Dr. Vidya Shankar and Dr. Sharadambal, who have studied deeply into the works of Sri Shyama Shastry, have all accepted this Varna as being a composition of Sri Shyama Shastry.
This Varna is also featured at Number 32 in Dr. T K Govinda Rao ’s book ‘ Compositions of Shyama Shastri..’ , published in 1997
Dr. Sharadambal also mentions that the Varna is included in the Hand Written Note Book of Shyama Shastry II (the great grandson of Sri Shyama Shastry).
Further, Sri Subbarama Dikshitar, in his Sangita-Sampradaya-Pradarshini (published in the year 1904), has included this Varna among the works of Sri Shyama Shastry. He has also worked out, in great detail, the Notations , spread over five pages, for the Taana Varna ‘Samini...’ pages 1540 to 1545 in the Appendix-Anubandha
*
Considering the fact that many scholars had gone into the issue; and had, after due consideration, admitted this Varna into the list of the compositions of Sri Shyama Shastry, we may perhaps follow suit.
But, we may, for a limited purpose, treat it as the sole representation of Madhura Bhakthi in his compositions , which came about at a very brief passing phase along the arduous course of his Sadhana; as it happened , later, in the life of Sri Ramakrishna.
**
This is a typical Ata-Taala-Varna, starting in the Laghu after a pause of eight Akshara-kala duration. The only difference being the Svarasahitya passages suffixed to the Muktayi Svara, first, fourth and fifth Ettugada-Svaras. There are five Ettugada Svaras in all. Few syllables are there in the Pallavi and Anupallavi with more vowel extensions
*
According to Smt. Sharadambal, who has made a detailed study of this Varna:
This Varna ‘Samini-ramm-anave’, though similar to Svarajati (pertaining to Dance) in structure has evolved with a separate Pallavi, Anupallavi and Mukthayi-Svara, collectively known as Purvanga. The Utaranga part consists of Carana, Carana-Svaras and Sahitya.
In the complete version of the Varna ‘Samini-ramm-anave’ (Anandabhairavi) as seen in the Note Book of Shyama Shastry II, there is no Sahitya for the Ettugada-Svara. The Carana and the Carana-Svaras are also missing.
But, in other books, the Sahitya is found for Ettugada-Svara and some Carana-Svaras.
Among the Carana-Svaras, the first, fourth and the fifth alone have Sahitya portions. The four Carana-Svaras have one Avarta; while, the last one has two Avartas. There is no Anubandha or the continuing portion after the Carana-Svara. After singing the last Carana-Svara and the Sahitya, the Ettugada-Pallavi is sung. Then, the Anubandha is sung; and, finally, the Varna is concluded with the singing of Pallavi.
*
The Graha-Svaras for the various Angas of this Varna ’Samini….’ (Anandabhairavi) are : Shadja for the Pallavi, Anupallavi and the Mukthayi Svara. The Carana starts as: ’ mg-Ma-ga-ma-Pa’, after ending the phase ‘Pa-dha-pa-ma-ga-ga’. The Carana is taken as ‘ga-ga-Ma’
While the first and second Ettugada-Svaras start on Pa; the third and fourth Svaras on Madhyamā; and, the fifth Svara on Nishada. The ending phases of the Svaras have natural link with Carana.
We can find different Svaras as the ending Notes. While the first and last Svaras end as ’ Sa-ga-ri-Ga-ga’ ; the second ends as’ Pa-Ma-Ga-Ri-Ni’; third as ‘Sa-Ni-Dha-Pa’; and, the fourth as ‘ Ma-Pa-Sa-Ni-Dha’. And, the Graha-Svara ‘Ma’ is sung with a glide (Jaru) from ‘Ga-Ni-Pa and Dha’.
*
As regards the Gamakas, the Varna ‘Samini..’ opens with the key phrase of Anandabhairavi Raga i.e., the ‘Erra-jaru’ prayoga as ‘ Sa/Sa Dha-Pa-Ma-Ga-Ma’ in the Pallavi and also in the Anupallavi, as ‘ Sa/Sa Dha-Pa-Ma’ as published in the Samgita-Sampradaya –Pradarshini of Sri Subbarama Dikshitar.
The Jaru-Prayoga is found not only as the opening phrase ; but also in the other parts of the composition.
*
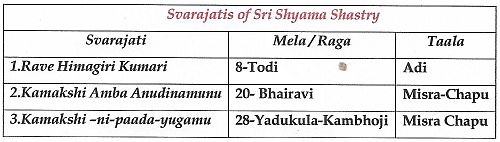
We find Svaraksharas in many places in the Varnas of Sri Shyama Shastry; as also in the Svarajatis.
In the two Varnas, Svarakshara syllables are found in the beginning as well as in some places. Both the Shuddha and Suchita Svaraksharas are found in them
In the Varna in Anandabhairavi Raga, Svaraksharas are found in the beginning of the Pallavi, Anupallavi and Carana.
[ I am reproducing here a rather lengthy observation / comment receive by mail from Vasudeva Anand.
I have been watching the ongoing debate concerning the Varna ‘Samini rammanave’ by Sri Shyama Shastry.
These are my tuppence, for whatever it is worth.
The revered Trinity of the Carnatic Music are all basically rooted in Bhakthi-Bhava. The Music for them was a means for expressing their devotion; and their Kritis were their offerings, like flowers, to their deities.
These composers of long-lasting musical careers also try to have in their repertoire other kinds of Rasas and Rasa-anubhavas. While their own essential attitudes stay firmly as bedrock, they might occasionally try other Bhavas as well. In other words; while Bhakthi is their Sthayi-Bhava, its variants like Madhura-Bhakthi would be its Sanchari-Bhava.
*
In the case of Sri Shyama Shastry ; all his compositions are in submission to the Mother Goddess praying for her Love and protection. All his Kritis are steeped in child-like devotion to its Mother. Perhaps his only composition depicting Madhura Bhakthi is the Varna ‘Samini rammanave.’
But the two of the Trinity – Sri Thyagaraja and Sri Mutthuswamy Dikshitar – have composed many Kritis (apart from those in Karuna and Bhakthi Rasas) , which portray different Rasas and Rasanu-bhava . Some of their songs do have Srngara Rasa.
For instance:
Sri Thyagaraja’s Nauka Charitam depicts the Nayaki-Bhava and has shades of Srngara Rasa. All the Gopis are Anya-nayikas depicting prouḍa and swādhina-pathika nāyikā-bhāva.
He describes the colourful scenes of the Gopis , dressing themselves , adorning themselves with lovely looking fragrant flowers to dance with Krishna : Shringārinchukoni-vedaliri-Sri-Krishnunithōnu…..-Puvvulumudugusunokathe….. Ravvajeyusu-nokathevētkaka
One of the Gopis is offering exotic flowers to Krishna, while another is offering him Tambūla. Some others are combing his hair, teasing him and making fun of him. While some are looking coyly at Krishna, someone suddenly hugs him overcome with love, some put Tilaka on his forehead, laughing and enjoying, calling him to sit beside them. All these lines in the song explain the essence of Srngara of the Madhura Bhakthi.
*
Further, some of his songs resemble Javalis. The songs of this genre describe the intimate relationship between the Nayaka and the Nayaki. Take, for instance, his songs Entha Muddhu and Chinna Natane, based in Nayika-Nayaka-bhedha. The song Chinna Natane, in particular, alludes to the relation between the Nayaka and the Nayaki.
In Entha Muddhu,
Sri Thyagaraja says : How charming and how elegant is He! Whoever is capable of describing! No matter how great people are, they became besieged by thoughts of lust. Being slaves to lust, they fear their mothers-in-law; yet, they pretend as true devotees of the Lord. Much like jug knowing the taste of milk! How charming and how elegant is He – praised by this Thyagaraja – who bears burden of the Universe! Whoever is capable of describing!
In Chinna Natane,
He says: Have you not taken me, clasping my hand from my childhood and accepted with grace numerous services from me? You had assured me of your care and protection to the last. Now it looks as if you are in two minds, unable to decide if you should accept me or abandon me to my fate. Please help me to uphold my self-respect at least as a devotee of yours. Oh Ocean of virtues! Transcendent Lord!
**
As regards Sri Mutthuswami Dikshitar his two Kritis- Kadambari Priyayai and Arunacha natham– do definitely differ from his other well known compositions steeped in Bhakthi and Vairagya Bhavas.
The Kriti Kadambari Priyayai is beautifully suited for an elaboration as a Padam in a Bharatha-natya recital. It brings nature and Srngara Rasa together beautifully. Its Kala pramana is eminently suited for Abhinaya.
In his other Kriti – Arunacha natham- Arunachala-Natham-smarami-anisamapeeta kuchamba- is based on Srngara. Sri Dikshitar brings out the Nayaka-Nayika-bedha in its all its expressions.
The sheer beauty of this piece lies in the fact the Nayaka-Nayika-bedha is ensconced within a larger Bhava of Madura Bhakti, wherein the Jeevatma and Paramatma are in union.
**
Here in all these cases, Srngara should be viewed as an aspect of Madhura Bhakthi; and , should not be taken as something that is improper .]

- Dayanidhe Mamava sadaa – Begada (29) Adi Taala
[Raga Begada is the Janya of the 9th Mela Dhira Shankarabharana
Arohana: s g r g m p d p S; Avarohana: S Nd p Mg r s
Svara-Sthanas: Shadja, Chatussruthi-Rshabha-, Antara-Gandhara-, Suddha-Madhyama, Panchama, Chatussruthi Daivata, Kakali Nishada]
The Dayanidhe (Begada, Adi Taala), comparatively, is a short Varna. Its Pallavi, Anupallavi and Carana, have just one line each. The Svarasahitya that follows the Carana has four lines.
The Vaggeyakara Mudra or Sva-nama, unusually, appears right at the beginning of the Varna in the Pallavi as: Dayanidhe mamava sadaa Shyama Krishna pujite.
This Varna in Sanskrit is a simple prayer, composed in easy flowing beautifully worded lines; very pleasant on the ears.
The Varna calls out to the Mother, citing her various names and forms (Nama-Rupa).It describes the beauty of Devi as having soft and delicate feet; and a very graceful neck.
Lalita-pada-yugale; kamaniya-kandhare
Sri Shyama Shastry sings the magnificence of the Mother, praising her as the protector of the people of the world, the Sages and all the celestial beings. And, as one who mitigates the sins of all beings; and, protects the virtuous
Parama-Pavani; Bhavani; Paratpari; Shiva-shankari / Palita-Jana-Munigana- Sura-samude / Paapa-shamani, Sahrudaya-sammodini/
He adores the Mother as the Ocean of mercy and compassion; the abode of all illustrious virtues, which bring delight to pious people. And, he prays to her to grant him the sublime virtue of devotion
Mahaniye-Sugunalaye -Vitara –Bhakthim me
This is a very pious, delightful and a happy song, praying to the Mother to protect, redeem and uplift all beings including the Munis (Sages) and Devas.
*
This is a Varna with vowel extensions in the Pallavi and Anupallavi, lending scope for Madhyamā Kala singing.
A Svarasahitya passage is appended to the Mukthayi Svara.
There are four Ettugada-Svaras in the Uttaranga.
There is no Sanchara below Madhya-Sthayi-Shadja in this Varna; but, there are many Tara-sthayi phrases.
The Svarakshara beauties can be seen in the Pallavi, Svarasahitya and the Carana.
[There is also another version of this Varna, which is generally sung with slight variations.
For more on this, please check page 251 0f Dr. Manju Gopal’s work under Appendix.]
*
Smt. Sharadambal , in her book, talks about this Varna
The Varna ‘Dayanidhe’ in Begada Raga is not found in the Hand-Written Note Book of Shyama Shastry II. This Varna as found in the book of Sri A Sundaram Ayyar is in the regular structure of Taana-Varna with Pallavi, Anupallavi and Mukthayi-Svara, in the Purvanga. And, the Uttaranga consists of a Carana and four Ettugada-Svaras.
Yet, we find the Sahitya for the Muktayi Svara, and the second Avarta for the Carana to be sung after the last Ettugada-Svaras in the book of Smt. Vidya Shankar
*
The Varna ‘Dayanidhe ‘ in Begada Raga of Sri Shyama Shastry , in praise of Goddess Raja-rajeshvari is in simple diction. In the Pallavi of the Varna itself, we find the Mudra of the composer, in the second Avarta.
The actual words start as Atita-Eduppu from the first Avarta as: ‘Sa //Dha Shyamakrishna’. Usually, the Mudra of the Vaggeyakara will figure in the Anupallavi of the Varna.
*
Both the Nishadas are used in the Begada Varna ‘Dayanidhe’. The Anya-Svara Kaishiki Nishada is used only in the opening phase: ’Dha-Pa-Ma-Pa-Dha-Ni-Dha-Pa’.
[The noted scholar Dr. V V Srivatsa in his ‘Introduction and historical background of the Begada ‘presented at the Raganubhava session on Begada Raga held on 16 January 2000, while referring to the compositions of Sri Shyama Shastry in that Raga mentions :
Begada is a Raga with unique, if not exclusive, Madhyama and Nishada Svaras. The Madhyama is of Pratyantara-Madhyama level. Nishada appears to be between the Kaishiki and Kakali-Nishada Svaras. This Raga also permits, on a selective basis, Kaisika and Kakali-Nishada. Begada is of the genre of Sahana, Saveri and Anandabhairavi, liked primarily for the Ranjakatva. The dual-vakra-sanchara in the Arohana is the main characteristic of this raga. The glide from the Purvanga to the Uttaranga is harmonious.
Begada belongs to a select group of Ragas in which we have at least one composition by each member of the Trinity. This is a raga which provides Hasya, Srngara and Adbhuta Rasas. The present version of this raga conforms to that given in the Sangraha Choodamani.
Earlier, in the Adi tala Varnam by Syama Sastri, we can find often, the permutation “pa-ma-ga-ri”. Syama-Sastri’s “Kamakshi-Nato-Vada” has several pristine sancharas now virtually lost to posterity.]
The Pallavi alone starts with ‘Dha’, while the Anupallavi and Ettugada –Svara start on Ma ; the Ettugada-Pallavi and the first two Svaras start on ’Pa’; third one on ‘Ga’; and, the last on Tara ‘Sa’.
Though in many Varnas we find similarity in the opening Svaras of the Pallavi and the Ettugada Svara here is missing.
*
We find Svaraksharas in many places in the Varnas of Sri Shyama Shastry; as also in the Svarajatis.
In the two Varnas, Svarakshara syllables are found in the beginning as well as in some places. Both the Shuddha and Suchita Svaraksharas are found in them
The Varna ‘Dayanidhe’ in Begada Raga also starts with Shuddha Svarakshara in all the three Angas.

- Nive gatiyeni namminanu Jagadamba– Kalyani (65) –Tisra Mathya
[Raga Kalyani is the 65th Melakarta Raga; Sampurna Raga It is also called as ‘Mecha Kalyani’ based on Katapayadi Sutram
Arohana: s r g m p d n S; Avarohana: S n d p m g r s
Svarasthanas: Shadja, Chatussruti Rshabha, Antara Gandhara, Prati Madhyama, Pachama, Chatussruti Daivata, Kakali Nishada]
In this Varna, Sri Shyama Shastry prays to the mother to listen to his pleas (manavi vinu); to make haste and come to him (vegame); and, to rescue him, since she is the only resort and there is none else to protect him.
He addresses the Mother Kanchi Kamakshi seated in Kama-Koti as Raja-Rajeshvari; Anatha-rakshaki (one who protects the orphaned)
O Jagadamba (mother of all this existence) I have been listening to your awe-inspiring legends (Charitamu-vini-vini); and have been constantly singing your glory (pogadi-pogadi). O Bangaru Kamakshi I have absolute faith in you (nere namminanu) and take refuge in your lotus feet (paada-kamala). You are my only saviour. Please do protect me.
The Raga Mudra and Vaggeyakara Mudra are in the phrase: Kalyani Shyamakrishna Sodari Devi.
The Telugu Sahitya is in simple words. It is the Music of the Varna that is more impressive.

What better way could there be to conclude the Series than with the auspicious , most pleasing and lovely Mangala-Kriti (Shankari-Shankari, Kalyani, Adi), recited by Sri Shyama Shastry as a benediction (Svasthi-vachana) – a prayer entreating the divine blessings of his Mother, the Supreme Goddess Raja-Rajeshvari, who is the very embodiment of all the spiritual knowledge (Tattva-jnana-rupini) and one who enlightens all (Sarva-chitta-bohini) to bless and grant (Disa) all of this existence (Sarva-Lokaya) health, happiness , prosperity (Jaya) and well-being in all its forms (Shubha)
– Mangalam– Jaya Mangalam – Shubha Mangalam
श्याम कृष्ण सोदरि शिशुं मां परिपालय शङ्करि
करि मुख कुमार जननि कात्यायनि कल्याणि
सर्व चित्त बोधिनि तत्त्व ज्ञान रूपिणि
सर्व लोकाय दिश मङ्गळं जय मङ्गळं
शुभ मङ्गळं (शङ्करि)


Sources and References
- Indian Culture, Art and Heritage by Dr. P. K. Agrawal
- Shodhganga chapter Six
- Shodhganga Chapter Seven
- Shodhganga Chapter VI
- Shodhganga Chapter VII
- Shodhganga handle
- A Voyage through Dēśa and Kāla
- Compositions of Shyama Shastri (1762-1827)
- Origin and development of Indian music
- https://archive.org/stream/composers00ragh/composers00ragh_djvu.txt
- https://archive.org/details/composers00ragh/page/46/mode/1up
- Prof. P. Sambamoorthy
- https://ebooks.tirumala.org/downloads/syamasasthri.pdf
- https://www.sangeethapriya.org/tributes/shyamakrishna/dl_krithis.html
- http://www.medieval.org/music/world/carnatic/shyama.html
- http://carnatica.net/special/shyama.pdf
- https://shodhganga.inflibnet.ac.in/bitstream/10603/173579/11/11_chapter%204.pdf
All images are taken from Internet




































 *
*